在上一篇文章中,我们本地已经能够运行起 Thoughtworks 新版本在线雷达。
也能够通过修改 JSON 文件来完成对内容的更新维护,但是距离好用的技术雷达还差很远,尤其是在对雷达图上的技术点、页面内容进行更新维护的时候。
本篇我们就继续来折腾,先从最复杂的雷达图部分开始吧。
回顾技术雷达页面细节
在继续进行定制修改前,需要先了解技术雷达的前端程序的实现方案、大概执行流程及一些原理。
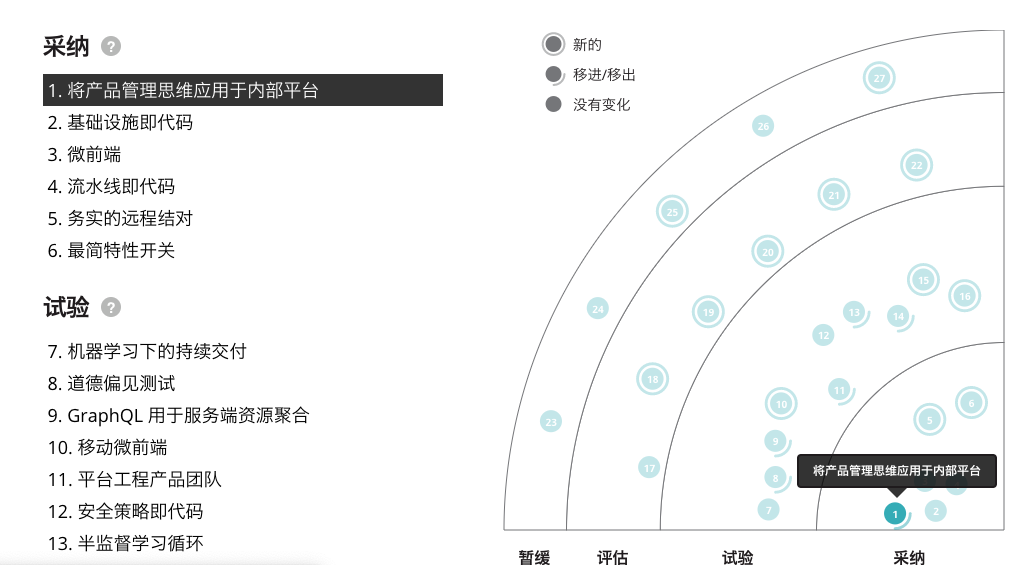
通过分析查看页面资源引用、脚本程序调用,页面模版、页面运行结果状态可以得到几个信息:
- 页面的雷达图是由 D3 在页面文档加载完成后,分析页面 DOM 结构中的数据异步渲染为 SVG 图,未使用当前流行的各种前端响应式数据方案。
- 页面雷达图中的坐标点和技术列表中的内容是通过数据中的 ID 字段进行一一对应的,不论对列表元素还是雷达点进行操作,都会关联选中状态到对应的元素上。
- 页面雷达图中的点的绘制坐标是经过定制公式计算得出,应该和我们提供的 JSON 数据中的方向角
θ和 半径r有关,通过简单修改数据内的theta和radius可以看到坐标有变化,但是不清楚其对应关系。
因为代码基本都被混淆过了,所以接下来我们需要开始一段简单的前端逆向过程。
探索雷达图的秘密
先从最难的技术点进行攻关:雷达图点坐标点的维护。实现让坐标点的添加、更新维护之类的操作,可以通过页面上“所见即所得”的方式来完成,而不需要修改 JSON 数据中的属性来碰运气。
从 SVG 方向入手
想要完成对点的坐标维护,首先要知道这些坐标点是怎么进行定位的。需要先观察 D3 生成的“可交互” SVG 的结构,结构示例代码:
<div id="quadrant">
<svg width="502" height="550"><path d="M-187.5,2.2962127484012872e-14A187.5,187.5 0 0,1 -3.4443191226019305e-14,-187.5L0,0Z" fill="#FFF" transform="translate(501, 500)" stroke="#808184" stroke-width="1px"></path><path d="M-343.75,4.2097233720690264e-14A343.75,343.75 0 0,1 -6.314585058103539e-14,-343.75L-3.4443191226019305e-14,-187.5A187.5,187.5 0 0,0 -187.5,2.2962127484012872e-14Z" fill="#FFF" transform="translate(501, 500)" stroke="#808184" stroke-width="1px"></path><path d="M-437.5,5.35782974626967e-14A437.5,437.5 0 0,1 -8.036744619404505e-14,-437.5L-6.314585058103539e-14,-343.75A343.75,343.75 0 0,0 -343.75,4.2097233720690264e-14Z" fill="#FFF" transform="translate(501, 500)" stroke="#808184" stroke-width="1px"></path>
...
<a class="quadrant-blip tooltipstered" id="blip-9142" xlink:href="techniques/infrastructure-as-code" style="text-decoration: none; cursor: pointer;"><g transform="scale(0.7352941176470589) translate(570.5566057222617, 635.8929373024487)" fill="#3DB5BE" class="adopt-blip"><circle r="15" cx="18" cy="18" opacity="1"></circle></g><text x="433.02691597225123" y="485.30363036944755" font-size="10px" font-style="normal" font-weight="bold" fill="white" style="text-anchor: middle;">2</text></a>
...
虽然页面真实存在的 SVG 图的结构和元素非常多,不过我们只需要关注具体的“点坐标”元素,那些带有 quadrant-blip tooltipstered 类名的 A 标签。可以看到元素的位置是写在 SVG 变换属性 transform 中的,通过设置其缩放属性 scale 和变形属性 transform 来玩的。
这里引申出了两个问题:
- 这里存在缩放情况,浏览器的坐标体系和 SVG 的坐标体系是否一致,如果不一致如何建立映射关系?
transform属性中的内容和我们的数据的关联是什么,是怎么计算出类似transform="scale(0.7352941176470589) translate(570.5566057222617, 635.8929373024487)"的结果的呢?
探索坐标体系找出关联
通过查找资料了解到 SVG 中使用 transform 坐标系,使用的坐标变换方式是线性变换。考虑到我们后续要使用浏览器做所见即所得的坐标维护,所以这里首先要推理浏览器坐标点和 SVG 坐标点的具体关系。
以页面雷达图中第一个点为参考系,写一段代码,用于获取 SVG 第一个节点的各种坐标信息,来辅助我们推理坐标体系关系。
const pictureContainer = document.querySelector("#quadrant svg");
const bodyContainer = document.body;
const firstPoint = document.querySelector("#quadrant svg a g");
let timer = [];
[pictureContainer, bodyContainer, firstPoint].forEach((container, idx) => {
container.addEventListener("mousemove", function (ev) {
if (timer[idx]) clearInterval(timer[idx]);
timer[idx] = setTimeout(function () {
console.group(container.tagName);
console.log(`全局坐标: [${ev.x}, ${ev.y}]`);
const rel = container.getBoundingClientRect();
console.log(`相对坐标: [${rel.x}, ${rel.y}]`, `元素偏移位置: left ${rel.left} top ${rel.top}`);
console.log(`相对偏移: left => ${rel.left} top => ${rel.top}`);
const props = container.getAttribute("transform");
if (props) {
const [scale, propX, propY] = props.match(/(\d+(\.\d+)?)/g);
console.log(`属性坐标: [${propX}, ${propY}]`);
}
console.groupEnd(container.tagName);
console.log();
}, 100);
});
});
在页面中执行上面的代码,并将鼠标移动到页面第一个坐标点上,可以看到类似下面的日志。
g
全局坐标: [1098, 326]
相对坐标: [1081.539306640625, 309.10345458984375] 元素偏移位置: left 1081.539306640625 top 309.10345458984375
相对偏移: left => 1081.539306640625 top => 309.10345458984375
属性坐标: [515.2133485777726, 639.4006860993144],缩放数值: 0.7352941176470589
svg
全局坐标: [1098, 326]
相对坐标: [700.5, -163.25] 元素偏移位置: left 700.5 top -163.25
相对偏移: left => 700.5 top => -163.25
BODY
全局坐标: [1098, 326]
相对坐标: [0, -924] 元素偏移位置: left 0 top -924
相对偏移: left => 0 top => -924
可以看到元素在 SVG 图中定位使用的属性坐标和我们全局捕捉鼠标使用的坐标数值有较大的差异,为了进一步判断,我们需要做一些额外的计算辅助推理:试着使用 SVG 元素的全局坐标和其相对元素偏移相减,发现数字还是偏差较大,试着直接用结果除缩放数值,得到 544.52 这个和属性坐标 515 相对较近的数值。
猜测这里有一定的偏移计算,结合 SVG 和 HTML 的定位体系都是基于元素左上角端点,这个日志采样点应该相对计算点位置偏“右下”,结果相比较属性值偏大应该是合理的。
为了完成程序,我们需要更得到准确的计算方式,也就是进一步探索上一小节中的第二个问题,这个坐标点是如何通过 JSON 文件中的角度和半径计算出来的。
逆向分析查找定位坐标算法
使用节点的属性作为关键词,我们定位到 /js/k8s_production/radar/quadrant.js 这个用于生成 SVG图的脚本程序。脚本原始内容,我在 GitHub 进行了一份存档,如果你感兴趣的话,可以访问这个地址。
前文提过,代码均被混淆压缩,所以这里我们需要先使用编辑器对代码进行格式化。因为坐标属性在 <g> 标签上,所以我们尝试使用以下关键词进行搜索定位:
<g>,尝试定位完整片段a g,a > g…,尝试定位 XPath 逻辑"g",尝试定位动态创建元素
最终,使用最后一个方式定位到了两段代码实现,为了后文叙述方便,我们这里给这两个函数起个名字,坐标点元素创建函数。
function R(t, a, e, r, i) {
if ($radar_chart_ft) {
var n = t.append("g").attr("transform", "scale(" + r / 34 + ") translate(" + (a * (34 / r) - 17) + ", " + (e * (34 / r) - 1) + ")");
...
function M(t, a, e, r) {
if ($radar_chart_ft) {
var i = t.append("g").attr("transform", "scale(" + r / 34 + ") translate(" + (a * (34 / r) - 17) + ", " + (e * (34 / r) - 1) + ")");
return i.append("circle").attr("r", "15").attr("cx", "18").attr("cy", "18"), i;
}
...
我们可以对这里的数值做一个简单的修改,比如将常量中部分 34 修改为 3.4,刷新页面,可以看到坐标点确实发生了变化,看来是找对了地方。
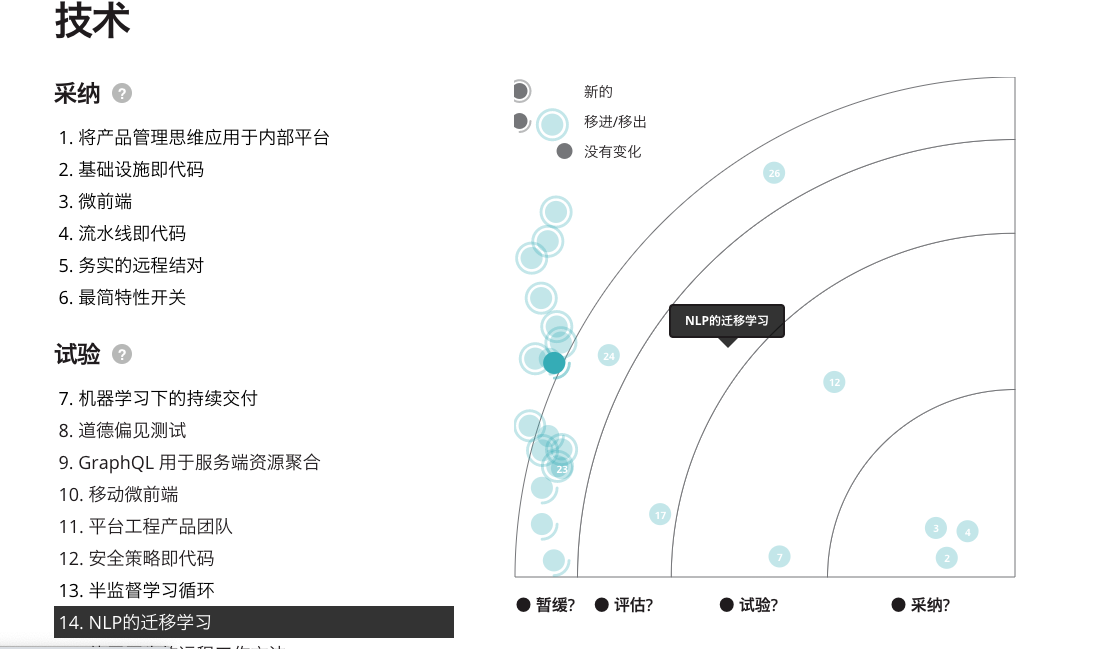
为什么这里会有两处实现呢?顺着文件往下翻找,不远处可以看到程序中对这两段函数的使用。
...
(m = $("#quadrant-blip-list").data("quadrant")),
(x = S.quadrantData[m]),
(0, { t: R, c: M }[h.movement])(_, v, g, y, x[h.blip_status])
.attr("fill", b)
.attr("class", h.ring.toLowerCase() + "-blip");
...
原来这里是根据 h.movement 这个字段,来对程序动态切换所需要的方法,结合应用交互,可以知道,这个字段描述的是有无“变更方向方式的技术点”。
确认了两个函数都是我们所需要处理的。对上面坐标点元素创建函数进行整理抽象,不难得到下面用于渲染最终的雷达点在 SVG 图中的公式,观察公式,果然存在之前小节中推测存在“偏移量”的情况。
// 用于创建不同趋势坐标点函数
function M(t, a, e, r) { ... }
function R(t, a, e, r, i) { ... }
// 相关公式,r / a / e 含义暂不清晰
// scale = r / 34
// x = a * (34 / r) - 17
// y = e * (34 / r) - 1
到这里,我们可以确定绘制具体的坐标点使用了直接坐标体系,但是还不清楚如何和数据中的极坐标体系(角度、半径)关联。
编写独立的直角坐标获取程序
既然我们期望的是所见即所得的方式来维护坐标点,那么需要为技术雷达添加一个新的能力:获取鼠标在页面 SVG 图上的任意坐标点,并转换为技术雷达程序内使用的坐标数值。
为了保障我们的工具正确有效,我们需找到“基准”参考,大白话说得知道每个坐标点在技术雷达中的计算结果,得有正确答案。
这里可以从技术雷达这个程序本身的交互入手,页面中有一个交互逻辑是当鼠标移动到坐标点上会和列表元素进行联动。所以可以考虑先从页面交互事件入手,对鼠标事件进行修改,让页面原始交互输出正确的坐标点计算结果。
继续翻看格式化后的代码,使用 "mouse 为关键词进行搜索,找到鼠标移动到技术雷达的点的时候的交互:
...
C.on("mouseenter", function () {
$("#blip-" + a.id).tooltipster("open"), F(a.id, "white");
}),
C.on("mouseleave", function () {
$("#blip-" + a.id).tooltipster("close"), A(a.id);
});
...
在 mouseenter 事件中添加一些代码,就可以辅助我们进行计算结果验证啦。
C.on("mouseenter", function () {
$("#blip-" + a.id).tooltipster("open"), F(a.id, "white");
const { x: pX, y: pY } = this.parentNode.getBoundingClientRect();
const { x, y } = this.getBoundingClientRect();
const { x: svgX, y: svgY } = this.getBBox();
console.log(`父元素坐标 [${pX}, ${pY}]`);
console.log(`子元素坐标 [${x}, ${y}]`);
console.log(`计算差值 [${x - pX}, ${y - pY}]`);
console.log(`BBox() [${svgX}, ${svgY}]`);
console.log("");
})
刷新页面,将鼠标移动至第一个技术坐标点上,可以看到输出日志类似下面这样:
父元素坐标 [700.5, 100]
子元素坐标 [1081.539306640625, 572.3534545898438]
计算差值 [381.039306640625, 472.35345458984375]
BBox() [381.03924560546875, 472.35345458984375]
这里细心的你会发现 getBoundingClientRect 和 getBBox 相比,精度第了不少,那么我们使用哪一个方法呢?答案是都可以。
进一步调整代码,将坐标和上文抽象的公式结合起来,在最后一个 console.log 前添加下面的内容。
const props = this.querySelector("g").getAttribute("transform");
if (props) {
const [scale, propX, propY] = props.match(/(\d+(\.\d+)?)/g);
console.log(`属性坐标: [${propX}, ${propY}],缩放数值: ${scale}`);
const delta = [(x - pX) / scale, (y - pY) / scale];
console.log("[计算偏移]", ...delta);
}
再次刷新页面,鼠标再次移动到第一个技术坐标点上,可以看到输出日志中的内容如下:
属性坐标: [515.2133485777726, 639.4006860993144],缩放数值: 0.7352941176470589
[计算偏移] 518.21345703125 642.4006982421874
可以看到实际已经很接近了,再添加一个偏移量修正,我们就基本可以实现一个和原来程序无关,在雷达图上指哪向哪里得到哪里坐标点的功能了。
保持之前对原始文件的修改,在控制台中运行下面的代码。
const radarContainer = document.querySelector("#quadrant svg");
const { x: radarX, y: radarY } = radarContainer.getBoundingClientRect();
const firstPoint = document.querySelector("#quadrant svg a g");
const { x: pointX, y: pointY } = firstPoint.getBoundingClientRect();
const pointProps = firstPoint.getAttribute("transform");
const [scale, pointPropX, pointPropY] = pointProps.match(/(\d+(\.\d+)?)/g);
if (!scale || !pointPropX || !pointPropY) throw new Error("template error");
function showInfo() {
console.log("[基准元素坐标]", pointX, pointY);
console.log("[基准元素属性]", pointPropX, pointPropY);
console.log("[雷达容器坐标]", radarX, radarY);
}
const delta = [(pointX - radarX) / scale, (pointY - radarY) / scale];
console.log("[获取容器内坐标]", ...delta);
const offsetFixs = [delta[0] - pointPropX, delta[1] - pointPropY];
console.log("[获取坐标偏移]", ...offsetFixs);
let timer = null;
// 人工定义偏移
const offsetCenterFix = [-18, -18];
radarContainer.addEventListener("mousemove", function (ev) {
if (timer) clearInterval(timer);
const { x, y } = ev;
timer = setTimeout(function () {
const groupLabel = `[${x}, ${y}]`;
console.group(groupLabel);
showInfo();
const delta = [(x - radarX) / scale, (y - radarY) / scale];
console.log("[获取容器内坐标]", ...delta);
const fixed = [delta[0] + offsetFixs[0], delta[1] + offsetFixs[1]];
console.log("[使用偏移量修正]", ...fixed);
const centerPoint = [fixed[0] + offsetCenterFix[0], fixed[1] + offsetCenterFix[1]];
console.log("[手动修正]", ...centerPoint);
console.groupEnd(groupLabel);
}, 100);
});
将鼠标移动到第一个技术点元素上,控制台会出现类似下面的日志输出:
[获取容器内坐标] 518.21345703125 642.4006982421874
[获取坐标偏移] 3.00010845347731 3.000012142873061
父元素坐标 [700.5, -282.25]
子元素坐标 [1081.539306640625, 190.10345458984375]
计算差值 [381.039306640625, 472.35345458984375]
BBox() [381.03924560546875, 472.35345458984375]
属性坐标: [515.2133485777726, 639.4006860993144],缩放数值: 0.7352941176470589
[计算偏移] 518.21345703125 642.4006982421874
[1094, 200]
[基准元素坐标] 1081.539306640625 190.10345458984375
[基准元素属性] 515.2133485777726 639.4006860993144
[雷达容器坐标] 700.5 -282.25
[获取容器内坐标] 535.16 655.8599999999999
[使用偏移量修正] 538.1601084534773 658.860012142873
[手动修正] 520.1601084534773 640.860012142873
第一和第三部分输出是我们在执行代码后,和使用鼠标和第一个技术雷达元素交互时输出的,第二部分输出是之前修改程序代码时输出的。可以看到通过手动修正程序,我们实现了:鼠标移动到技术雷达元素,得到其在 SVG 中具体 transform 后坐标点。
让坐标和数据进行联动
至此我们解决了前文中提到的 80% 的问题,现在只需要想办法让我们的数据和这个坐标点程序联动起来就好啦:想办法处理探究极坐标和直角坐标的转换。
逆向分析极坐标和直角坐标转换
继续回顾之前的坐标点元素创建函数,观察传递参数并查找实际的调用位置。
(h = a),
(_ = C),
(b = e),
(v = w.x),
(g = w.y),
(y = l),
(m = $("#quadrant-blip-list").data("quadrant")),
(x = S.quadrantData[m]),
(0, { t: R, c: M }[h.movement])(_, v, g, y, x[h.blip_status])
这里看到 (_, v, g, y, x[h.blip_status]) 是最终实际传递的参数,结合前文公式,我们可以将重点放在前四个参数 _, v, g, y 的来源上,认真观察上文,刚刚的代码处有一段赋值代码,可以看出变量 w 就是计算后的数值,故接下来要关注的变量列表为:C, w(x,y), l 三个家伙、四个数值。不过再次观察 坐标点元素创建函数,发现第一个数值是 DOM 容器节点,所以可以忽略掉这个元素,只分析 w, l两个元素是什么来头就够了。
基于变量需要先声明后使用的特点,我们向上翻动,查找这两个变量。会定位到这段代码实现:
function l(a, t, e, r, i, n, o, l, c) {
var s, d, p, u, f, h, _, b, v, g, y, m, x,
w = ((s = a), (d = r), (p = i), (u = n), (f = o),
$radar_chart_ft
? { x: Math.abs(Math.abs(s.radius * d * Math.cos(z(s.theta))) - u * p), y: Math.abs(Math.abs(s.radius * d * Math.sin(z(s.theta))) - (f * p - (0 === f ? 15 : 0))) }
: { x: Math.abs(Math.abs(s.radius * d * Math.cos(z(s.theta))) - u * p), y: Math.abs(Math.abs(s.radius * d * Math.sin(z(s.theta))) - f * p) }),
...
从这里可以看到变量 w 会根据情况进行选择一段公式方案进行计算。
看到这里可能你会问,这里有两段公式,我们到底该使用哪段公式呢?结合之前的坐标点元素创建函数,我们可以推断,在雷达技术点定位绘制场景下,$radar_chart_ft 变量一定有值,所以公式应选择第一段:
{
x: Math.abs(Math.abs(s.radius * d * Math.cos(z(s.theta))) - u * p),
y: Math.abs(Math.abs(s.radius * d * Math.sin(z(s.theta))) - (f * p - (0 === f ? 15 : 0))),
}
变量 l 是这个块级函数 function l(a, t, e, r, i, n, o, l, c) 的第八个参数,将上述公式和代码实现进行梳理,可以看到我们的变量追踪名单上又多了一些。
- 公式参数
s,块函数第一个参数a,包含半径和角度数值 - 公式参数
d,块函数第四个参数r - 公式参数
p,块函数第五个参数i - 公式参数
u,块函数第六个参数n - 公式参数
f,块函数第七个参数o - 块函数第八个参数
l - 未出现定义的函数
z
看了这么多你一定很晕,我重新整理了一些伪代码实现帮助你理解这个过程。
// 1. 执行绘制坐标的具体函数
// 我们需要分析的是 a, e, r 三个数值的含义
function M(t, a, e, r) { ... }
function R(t, a, e, r, i) { ... }
// 获取坐标点计算公式
// scale = r / 34
// x = a * (34 / r) - 17
// y = e * (34 / r) - 1
// ---
// 2. 绘制函数的调用入口
...
(0, { t: R, c: M }[h.movement])(_, v, g, y, x[h.blip_status])
// 需要关注 _, v, g, y 四个变量,
// 结合上下文分析,我们只需关注调用函数中的 w, l 两个变量
/// ---
// 3. 角坐标计算函数
function l(a, t, e, r, i, n, o, l, c) { ... }
// 需要关注以下内容
//s = a, 函数第一个参数,包含半径和角度
//d = r, 函数第四个参数
//p = i, 函数第五个参数
//u = n, 函数第六个参数
//f = o, 函数第七个参数
//l 函数第八个参数
//z 未出现定义的函数依赖
首先找到未定义函数 z 的实现,看起来是一个角弧度转换公式,所得结果是 t 度的角:
function z(t) {
return (t * Math.PI) / 180;
}
我们再来看看函数是怎么被调用的呢?
{
x: Math.abs(Math.abs(s.radius * d * Math.cos(z(s.theta))) - u * p),
y: Math.abs(Math.abs(s.radius * d * Math.sin(z(s.theta))) - (f * p - (0 === f ? 15 : 0))),
}
搜索弧度角度转换,网上有一个 2016 年的小初高数学题答案把饭喂到了嘴边。
// 感谢作业帮,帮我回忆起了小初高数学 link: https://www.zybang.com/question/facb13a37dd8dc2f65a55d62ffea2f5a.html
∵ 弧度和角度换算:1°=π/180 rad
∴ sin(πα/180)=sinα
所以上面公式中的 z 函数调用,也可以不需要继续关注了。
接着以 l( 为关键词进行搜索,找到这个包含大量未解之谜的函数的调用实现,只有一处:
_(t).each(function (t) {
_(t.blips).each(function (t) {
l(t, a, r.colour, i, S.quadrantRadius, r.tx, r.ty, S.blipWidth, S.blipFontSize);
});
}),
看逻辑就能脑补出来程序兢兢业业跑循环将各种数据转换为实际坐标的执行过程,我们继续展开这段实现,对刚刚没有看到源头的变量都进行分析梳理。
var a = d3.select("#quadrant").insert("svg", ":first-child").attr("width", S.graphWidth).attr("height", S.graphHeight), t = s();
if (void 0 !== t) {
var e = $("#quadrant-blip-list").data("quadrant"),
r = S.quadrantData[e],
i = S.quadrantRadius / S.maxRadius;
n(a, 0, S.quadrantRadius, i, S.segmentData, r.startAngle, r.tx, r.ty, S.textColour),
_(t).each(function (t) {
_(t.blips).each(function (t) {
l(t, a, r.colour, i, S.quadrantRadius, r.tx, r.ty, S.blipWidth, S.blipFontSize);
});
}),
...
我们关注的参数序号为: 1, 4, 5,6, 7, 8,再次观察这些参数的引用来源:
第一个参数 t = s();
第四个参数 i = S.quadrantRadius / S.maxRadius;
第五个参数 S.quadrantRadius
第六个参数 r.tx
第七个参数 r.ty
第八个参数 S.blipWidth
可以看到,我们依赖的内容基本集中在了未知函数 s() 以及对象 r{tx,ty} 和对象 S{quadrantRadius,maxRadius,blipWidth} 三个内容上。
阅读源码,函数 s() 实现了一个序列化 DOM 数据的功能,和上篇文章中“提取并整理页面中的数据”小节大同小异,和函数 z 一样,接下来也不再需要继续关注这个函数。
function s() {
var a = [];
return (
$("#quadrant-blip-list")
.children("div")
.toArray()
.forEach(function (e) {
var r = [];
$(e)
.find(".blip-link")
.toArray()
.forEach(function (t) {
var a = {
radius: $(t).data("radius"),
theta: $(t).data("theta"),
movement: $(t).data("movement"),
blip_status: $(t).data("blipStatus"),
id: $(t).data("blip-id"),
ring: $(e).attr("id"),
radarId: $(t).data("radar-id"),
nameUrl: $(t).data("url"),
eventCategory: $(t).data("event-category"),
eventLabel: $(t).data("event-label"),
eventAction: "Click to Blip",
};
r.push(a);
});
var t = { blips: r };
a.push(t);
}),
a
);
}
继续追查变量 r,可以看到下面的代码实现:
var e = $("#quadrant-blip-list").data("quadrant"),r = S.quadrantData[e],
...
变量 r 根据当前雷达名称,从 S.quadrantData 中获取数据,正好就只剩这最后一个变量需要分析啦,查找 S = 定位到源码:
var S = {
graphHeight: $radar_chart_ft ? 550 : 500,
graphWidth: $radar_chart_ft ? 502 : 500,
quadrantRadius: 500,
blipWidth: 25,
blipFontSize: "10px",
blipColours: { adopt: "#44b500", trial: "#859900", assess: "#99df00", hold: "#bb5500" },
textColour: "#221D1F",
maxRadius: 400,
segmentData: [
{ title: t[0], startRadius: 0, endRadius: 150, colour: $radar_chart_ft ? "#FFF" : "#BFC0BF" },
{ title: t[1], startRadius: 150, endRadius: 275, colour: $radar_chart_ft ? "#FFF" : "#CBCCCB" },
{ title: t[2], startRadius: 275, endRadius: 350, colour: $radar_chart_ft ? "#FFF" : "#D7D8D6" },
{ title: t[3], startRadius: 350, endRadius: 400, colour: $radar_chart_ft ? "#FFF" : "#E4E5E4" },
],
quadrantData: cobra.quadrant_setup(),
};
我们继续需要分析的字段有:quadrantRadius,maxRadius,blipWidth 以及 quadrantData(包含tx,ty)。因为前三个字段都是写死的常量,最后一个函数调用了 cobra.quadrant_setup() 来获取结果。
现在所有的未解之谜就只剩 quadrant_setup 了,以这个关键词为结果进行搜索,定位到代码是另外一段常量定义:
((cobra = cobra || {}).quadrant_setup = function () {
"use strict";
return {
tools: { startAngle: 0, tx: 0, ty: 1, colour: "#83AD78", move_in: "bottomLeft", move_out: "topRight" },
"languages-and-frameworks": { startAngle: 90, tx: 0, ty: 0, colour: "#8D2145", move_in: "topLeft", move_out: "bottomRight" },
platforms: { startAngle: 180, tx: 1, ty: 0, colour: "#E88744", move_in: "topRight", move_out: "bottomLeft" },
techniques: { startAngle: 270, tx: 1, ty: 1, colour: "#3DB5BE", move_in: "bottomRight", move_out: "topLeft" },
};
})
这里根据页面名称,动态返回 tx和ty 两个变量的数值,结合雷达图不难猜到,这几个数值区分了平面的四个象限。
至此所有的“黑盒逻辑”就都浮出水面啦,我们将线索进行梳理还原整个计算过程。
完整的计算过程
结合上下文,我们不难写出完整的计算过程。
var S = {
quadrantRadius: 500,
blipWidth: 25,
maxRadius: 400,
quadrantData: {
tools: { tx: 0, ty: 1 },
"languages-and-frameworks": { tx: 0, ty: 0 },
platforms: { tx: 1, ty: 0 },
techniques: { tx: 1, ty: 1 },
},
};
// 这里根据页面实际情况获取,此处为 Mock
const mockGetPageType = () => "techniques";
const pageType = mockGetPageType();
const { tx, ty } = S.quadrantData[pageType];
function getPosByPolarCoords(theta, radius) {
const scale = S.quadrantRadius / S.maxRadius;
function z(t) {
return (t * Math.PI) / 180;
}
const pos = {
x: Math.abs(Math.abs(radius * scale * Math.cos(z(theta))) - tx * S.quadrantRadius),
y: Math.abs(Math.abs(radius * scale * Math.sin(z(theta))) - (ty * S.quadrantRadius - (0 === ty ? 15 : 0))),
};
const { x: a, y: e } = pos;
const r = S.blipWidth;
return {
scale: r / 34,
x: a * (34 / r) - 17,
y: e * (34 / r) - 1,
};
}
可以套入第一个技术点的数值"radius": 90, "theta": 165 进行计算,会得到和页面程序运行后 SVG 节点属性一致的数值:
{
scale: 0.7352941176470589,
x: 515.2133485777726,
y: 639.4006860993144
}
编写逆计算函数
有了上面一堆推导和梳理,我们接下来就可以编写逆计算实现了,首先是根据坐标点和给定的半径求角度值:
function getThetaByPropsPos(propX, radius) {
const x = (propX + 17) / (34 / S.blipWidth);
const scale = S.quadrantRadius / S.maxRadius;
function reverseZ(t) {
return (t * 180) / Math.PI;
}
function reverseAbs(a, b) {
return Math.abs(a - b) * -1;
}
return Math.round(reverseZ(Math.acos(reverseAbs(x, tx * S.quadrantRadius) / (radius * scale))));
}
然后是通过坐标点和给定的角度值计算半径:
function getRadiusByPropsPos(propX, theta) {
const x = (propX + 17) / (34 / S.blipWidth);
const scale = S.quadrantRadius / S.maxRadius;
function z(t) {
return (t * Math.PI) / 180;
}
function reverseAbs(a, b) {
return Math.abs(a - b) * -1;
}
return Math.round((radius = reverseAbs(x, tx * S.quadrantRadius) / (scale * Math.cos(z(theta)))));
}
看到这里你一定会疑问,数值计算拆成了两个函数,涉及两种未知数(直角坐标系坐标和极坐标系数值),而我们之前编写的程序只能使用直角坐标,好像程序串不起来嘛。
别着急,接下来我们就来完成剩余的部分。
编写独立的极坐标数据获取程序
下面这段程序实现了如何使用鼠标从技术雷达图上获取角度坐标。
const calcDegree = function (params) {
const { pos, origin } = params;
const x = pos.x - origin.x;
const y = origin.y - pos.y;
return Math.abs(Math.atan2(y, x) / (Math.PI / 180));
};
const alignment = document.querySelector("#quadrant svg path");
const eventArea = document.querySelector("#quadrant svg");
eventArea.addEventListener("mousemove", function (ev) {
const { top, left, width, height } = alignment.getBoundingClientRect();
const { x, y } = ev;
const p = calcDegree({ pos: { x, y }, origin: { x: left + width, y: top + height } });
console.log(p);
});
程序执行后,我们把鼠标在雷达图上随便移动下,将看到类似下面的内容:
159
160
161
162
...
需要注意的是,在获取直角坐标的程序里,我们的坐标的原点是从左上角开始的,而计算度数的时候,我们需要从右下角开始计算。不过 D3 生成的 SVG 的右下角并非我们看到的雷达图形的原点位置,雷达图包含了图表说明等元素,所以取元素数值的时候,可以通过获取我们看到的雷达图的元素的右下顶点。
现在,我们已经集齐了龙珠,可以开始召唤神龙啦。
编写完整的雷达图技术坐标点辅助程序
为了能够得到动态获取用户页面当前鼠标坐标点,并生成 JSON 数据所需要的极坐标 theta 和 radius 程序,我们需要将上面几段程序合,并做适当调整:
const radarContainer = document.querySelector("#quadrant svg");
const { x: radarX, y: radarY } = radarContainer.getBoundingClientRect();
const alignmentConatiner = document.querySelector("#quadrant svg path");
const alignData = alignmentConatiner.getBoundingClientRect();
const alignPos = { x: alignData.left + alignData.width, y: alignData.top + alignData.height };
const firstPoint = document.querySelector("#quadrant svg a g");
const { x: pointX, y: pointY } = firstPoint.getBoundingClientRect();
const pointProps = firstPoint.getAttribute("transform");
const [scale, pointPropX, pointPropY] = pointProps.match(/(\d+(\.\d+)?)/g);
if (!scale || !pointPropX || !pointPropY) throw new Error("template error");
const cons = {
quadrantRadius: 500,
blipWidth: 25,
maxRadius: 400,
quadrantData: {
tools: { tx: 0, ty: 1 },
"languages-and-frameworks": { tx: 0, ty: 0 },
platforms: { tx: 1, ty: 0 },
techniques: { tx: 1, ty: 1 },
},
};
const pageType = document.querySelector("#quadrant-blip-list").getAttribute("data-quadrant");
const { tx, ty } = cons.quadrantData[pageType];
function getRadiusByPropsPos(propX, theta) {
const x = (propX + 17) / (34 / cons.blipWidth);
const scale = cons.quadrantRadius / cons.maxRadius;
function z(t) {
return (t * Math.PI) / 180;
}
function reverseAbs(a, b) {
return Math.abs(a - b) * -1;
}
return Math.round((radius = reverseAbs(x, tx * cons.quadrantRadius) / (scale * Math.cos(z(theta)))));
}
function calcDegree(params) {
const { pos, origin } = params;
const x = pos.x - origin.x;
const y = origin.y - pos.y;
return Math.abs(Math.atan2(y, x) / (Math.PI / 180));
}
function showInfo() {
console.log("[基准元素坐标]", pointX, pointY);
console.log("[基准元素属性]", pointPropX, pointPropY);
console.log("[雷达容器坐标]", radarX, radarY);
}
const delta = [(pointX - radarX) / scale, (pointY - radarY) / scale];
console.log("[获取容器内坐标]", ...delta);
const offsetFixs = [delta[0] - pointPropX, delta[1] - pointPropY];
console.log("[获取坐标偏移]", ...offsetFixs);
let timer = null;
// 人工定义偏移
const offsetCenterFix = [-18, -18];
const degFix = -3;
radarContainer.addEventListener("mousemove", function (ev) {
if (timer) clearInterval(timer);
const { x, y } = ev;
timer = setTimeout(function () {
const groupLabel = `[${x}, ${y}]`;
console.group(groupLabel);
showInfo();
const delta = [(x - radarX) / scale, (y - radarY) / scale];
console.log("[获取容器内坐标]", ...delta);
const fixed = [delta[0] + offsetFixs[0], delta[1] + offsetFixs[1]];
console.log("[使用偏移量修正]", ...fixed);
const centerPoint = [fixed[0] + offsetCenterFix[0], fixed[1] + offsetCenterFix[1]];
console.log("[手动修正]", ...centerPoint);
const degree = calcDegree({ pos: { x, y }, origin: alignPos });
console.log("[当前度数]", Math.round(degree));
console.log("[半径结果]", getRadiusByPropsPos(centerPoint[0], degree + degFix));
console.groupEnd(groupLabel);
}, 100);
});
在页面内执行上面的程序后,鼠标移动到雷达图上的一个新的位置,我们能够看到输出内容包含了我们所需要的角度和半径。
[1024, 431]
[基准元素坐标] 1005.7625732421875 427.2989807128906
[基准元素属性] 521.6371496109771 564.5266208680346
[雷达容器坐标] 620 10
[获取容器内坐标] 549.4399999999999 572.56
[使用偏移量修正] 552.4399499983979 575.5599929014966
[手动修正] 534.4399499983979 557.5599929014966
[当前度数] 141
[半径结果] 102
将数值更新到 JSON 文件后,我们再次执行前篇文章中的页面生成脚本,刷新页面,可以看到坐标点已经符合我们的“指哪打哪”的要求啦。
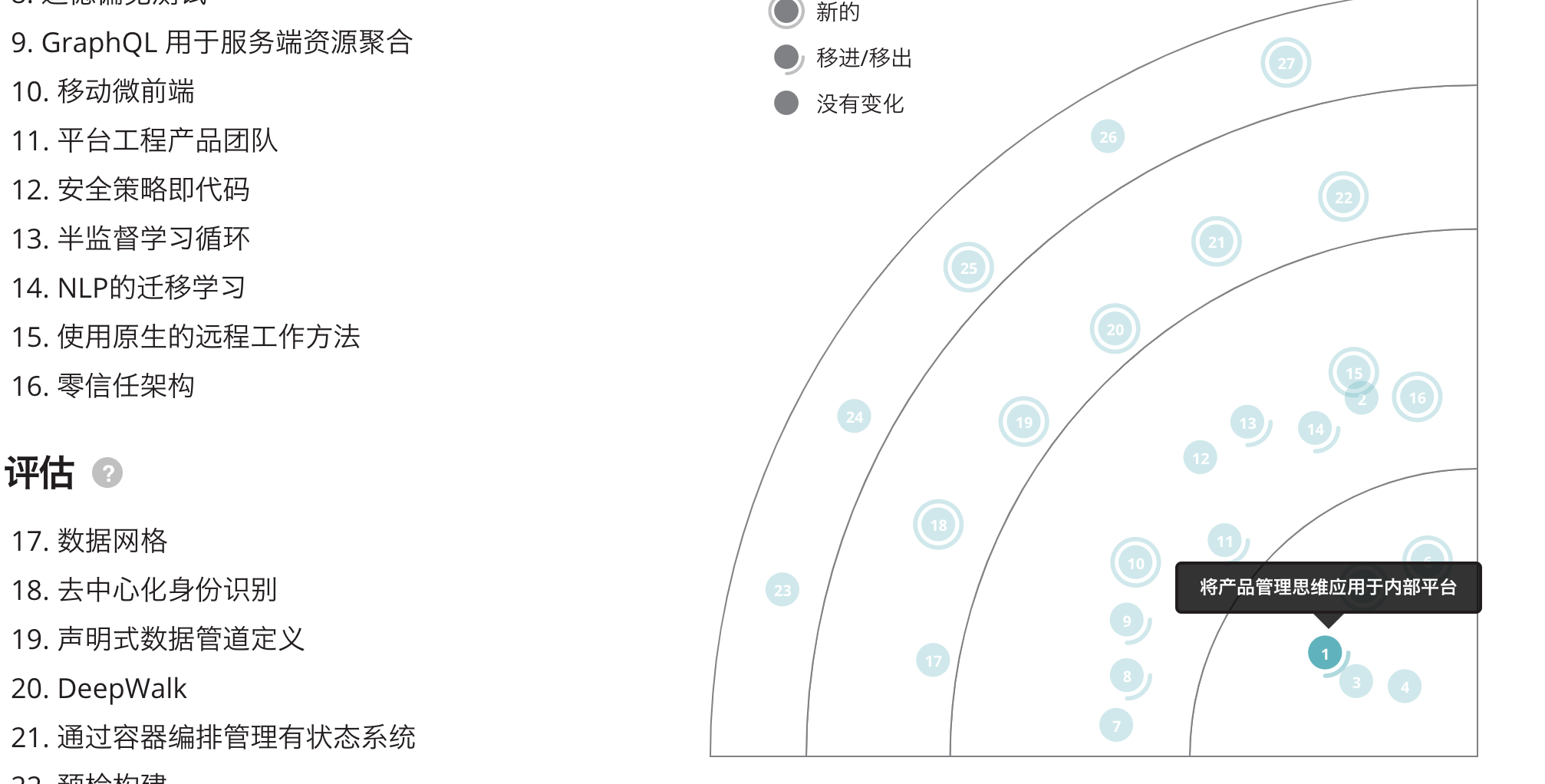
不过需要注意的是,因为原始的雷达程序实现原本就存在各种偏移量设定,所以我们得到的长度数值在后期还需要一定的调整。这里可以通过优化程序算法,或者在页面添加一个半径滑块控件来优化我们的坐标点维护体验。
另辟蹊径
这里讲一下另外一个解决方案,除了科学计算这种方式之外,我们还可以使用统计的思路,通过制作包含所有有效坐标点的数据表,来解决不易维护坐标点的问题。
获取当前程序有效的坐标点取值范围十分简单:
const { readdirSync, readFileSync } = require("fs");
const dataSource = readdirSync("./app/data")
.filter((file) => file.endsWith(".json"))
.map((file) => JSON.parse(readFileSync(`./app/data/${file}`, "utf-8")))
.reduce((prev, stageList) => {
return prev.concat(
stageList
.map((stage) =>
stage.data.map((item) => {
const { theta, radius } = item;
return { theta, radius };
})
)
.flat()
);
}, []);
const getRange = () => {
const sortByTheta = [].concat(dataSource).sort((a, b) => a.theta - b.theta);
const sortByRadius = [].concat(dataSource).sort((a, b) => a.radius - b.radius);
return {
theta: [sortByTheta[0].theta, sortByTheta[sortByTheta.length - 1].theta],
radius: [sortByRadius[0].radius, sortByRadius[sortByRadius.length - 1].radius],
};
};
console.log(getRange());
执行后得到结果:
{
theta: [ 7, 351 ], radius: [ 60, 385 ]
}
可以看到取值都是正整数,写两个循环,我们要的字典就出来啦,然后通过上面的直角坐标算法,求出这些数值组合的真实坐标数值,在鼠标事件上响应用户交互即可。
最后
写到这里,基于 thoughtworks 新版本的技术雷达最麻烦的部分就结束啦,下一篇技术雷达相关的内容,我会讲这个定制文章完整收尾。
–EOF